Medidas de forma - Asimetría y Curtosis

Asimetría (o Skewness)
Nos permite identificar si los datos se distribuyen de forma uniforme alrededor de la media aritmética.  Se mide a través del coeficiente de asimetría o de Fisher.  

Figura A                             Figura B

La figura A exhibe datos distribuidos normalmente, que por definición denotan simetría.  Al dibujar una línea por el medio del histograma, puede verificarse que un lado es el reflejo del otro.  La figura B es también simétrica, a pesar de que dista de ser normal.  Los datos simétricos reflejan un coeficiente de asimetría o de Fisher igual a cero.

Distribuciones asimétricas positivas o hacia la derecha

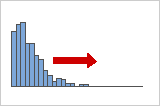
Los datos con asimetría positiva o hacia la derecha se llaman así porque la "cola" de la distribución apunta hacia la derecha y porque el valor de la asimetría es mayor a 0 (medido a través del coeficiente de asimetría o de Fisher).  Los datos sobre salarios suelen ser asimétricos de esta manera: muchos empleados comienzan ganando relativamente poco, mientras que pocas personas ganas salarios muy elevados.  La moda es menor a la mediana, y la mediana es menor a la media.  Los inversores estarían interesados en distribuciones asimétricas positivas ya que la media es mayor a la mediana.

Distribuciones asimétricas negativas o hacia la izquierda

Los datos asimétricos hacia la izquierda o con asimetría negativa se llaman así porque la "cola" de la distribución apunta hacia la izquierda y porque producen un valor de asimetría negativo (medido a través del coeficiente de asimetría o de Fisher). Los datos de tasas de fallas suelen ser asimétricos a la izquierda. Consideremos el caso de los focos: muy pocos se quemarán inmediatamente, la gran mayoría dura un tiempo considerablemente largo.  La moda es mayor a la mediana, y la mediana es mayor a la media.

Curtosis

Permite medir cuán concentrados están los datos alrededor de la media (el grado de concentración).  En otras palabras, si hay muchos datos agrupados cerca de la media.  Se mide a través del coeficiente de Curtosis.

Si este coeficiente es nulo, la distribución se dice normal (similar a la distribución normal de Gauss) y recibe el nombre de mesocúrtica.

Si el coeficiente es positivo, la distribución se llama leptocúrtica, más puntiaguda que la anterior. Hay una mayor concentración de los datos en torno a la media.  

Tiene colas "más anchas" que la normal (fat tails), ya que hay presencia de valores extremos.  El riesgo de curtosis en finanzas hace referencia a este tipo de distribución.

Si el coeficiente es negativo, la distribución se llama platicúrtica y hay una menor concentración de datos en torno a la media. sería más achatada que la primera.