Medidas de dispersión
Además de conocer donde están centrados los datos (con las medidas de tendencia central), debemos conocer la dispersión que tienen (en torno a la media). En finanzas, es común asociar dispersión con riesgo.
Medidas de dispersión: Rango, Desviación, Varianza, Coeficiente de variación, Ratio de Sharpe.
1) Rango. Es la diferencia entre el valor máximo y el valor mínimo en un set de datos.
Rango = Máximo valor - Mínimo valor
Posee como ventaja la facilidad de cómputo, pero como desventaja que utiliza únicamente dos piezas de la información de la distribución.
2) Desviación media absoluta. Las medidas de dispersión pueden contemplar en sus cálculos todas las observaciones en la distribución (más allá del valor máximo y mínimo, como utiliza el rango). La pregunta es ¿Cómo medimos la dispersión? Una noción básica es la distancia de una observación en torno a la media (Xi - X raya). La desviación media absoluta se basa en tomar el promedio de las desviaciones, y a las desviaciones aplicarles un módulo para volverlas valores absolutos.
3) Una segunda aproximación para cubrir el problema de valores negativos, es elevar las diferencias al cuadrado. Aquí aparecen la varianza y la desviación estándar.
La varianza es el promedio del cuadrado de las desviaciones alrededor de la media.
La desviación estándar es la raíz cuadrada de la varianza.
Varianza poblacional
Desvío poblacional
Varianza muestral
Donde X raya es la media muestral, y n-1 refiere a los grados de libertad cuando se estima la varianza poblacional.
Desviación estándar muestral
Donde X raya es la media muestral.
Semi-Varianza y Semi-Desviación
La varianza o desviación estándar de los retornos son usualmente interpretados como medidas de riesgo de un activo. Contemplan las dispersiones por arriba, y por abajo, de la media, pero los inversores están únicamente preocupados con el riesgo debajo (retornos por abajo de la media). Como resultado, se ha desarrollado la semi-varianza y semi-desviación.
Para el cómputo:
1) Calcular la media muestral
2) Identificar las observaciones que son menores a la media (descartar las observaciones que son igual o mayores a la media); suponer n* observaciones menores a la media.
3) Computar la sumatoria del cuadrado de las dispersiones en torno a la media.4) Dividir por n*-1. La fórmula para la semi-varianza es:
Coeficiente de Variación
La desviación estándar es más sencilla de interpretar que la varianza, ya que está expresada en las mismas unidades que las observaciones (en la varianza, las observaciones se elevan al cuadrado). Podemos encontrarnos con que es difícil interpretar que significa la desviación estándar en términos de variabilidad cuando miramos diferentes set de datos, debido a que cada set de datos posee una media diferente, o los otros set de datos pueden estar expresados en diferentes unidades. El coeficiente de variación resulta una herramienta útil en estas situaciones. Por ello, es que se referencia al coeficiente de variación como una medida de dispersión relativa.
A continuación, ilustramos un ejemplo de dos set de muestras, con medias marcadamente diferentes.
Muestra A: 50, 75, 65, 90
Media muestral: 70
Desvío muestral: 16,8
Muestra B: 800, 825, 815, 840
Media muestral: 820
Desvío muestral: 16,8
En la primera muestra, la observación más grande, 90, es un 80% más grande que la observación más chica, 50.
En la segunda muestra, la observación más grande, 840, es un 5% más grande que la observación más chica, 800.
Informalmente, un desvío muestral de 16,8 refleja un alto nivel de variabilidad relativa a la primera muestra, cuya media es 70. Pero un bajo nivel de variabilidad relativa a la segunda, cuya media es 820.
El coeficiente de variación puede calcularse a través de:
Medidas de dispersión: Rango, Desviación, Varianza, Coeficiente de variación, Ratio de Sharpe.
1) Rango. Es la diferencia entre el valor máximo y el valor mínimo en un set de datos.
Rango = Máximo valor - Mínimo valor
Posee como ventaja la facilidad de cómputo, pero como desventaja que utiliza únicamente dos piezas de la información de la distribución.
2) Desviación media absoluta. Las medidas de dispersión pueden contemplar en sus cálculos todas las observaciones en la distribución (más allá del valor máximo y mínimo, como utiliza el rango). La pregunta es ¿Cómo medimos la dispersión? Una noción básica es la distancia de una observación en torno a la media (Xi - X raya). La desviación media absoluta se basa en tomar el promedio de las desviaciones, y a las desviaciones aplicarles un módulo para volverlas valores absolutos.
La varianza es el promedio del cuadrado de las desviaciones alrededor de la media.
La desviación estándar es la raíz cuadrada de la varianza.
Varianza poblacional
Donde M es la media poblacional y N el tamaño de la población. Usar la media como parámetro de las diferencias (y no otra observación de la muestra), asegura que se obtenga la menor varianza (es una función convexa, y la media es un mínimo).
Bis: Si multiplico todas las observaciones por una constante, la varianza se multiplica por la constante al cuadrado.
Bis - Demostración:
Si multiplico las observaciones Xi por una constante C, entonces la media M pasa a multiplicarse. La misma demostración es aplicable para la varianza muestral.
Donde M es la media poblacional.
Tanto la varianza poblacional como el desvío poblacional son considerados parámetros de una distribución. Usualmente no conocemos la media de una población, por el hecho práctico de que no podemos conseguir datos de cada miembro en una población. Lo que se hace es intentar estimar la media poblacional, a partir de una muestra tomada de la población. Luego, se procede a calcular la varianza muestral y el desvío muestral, utilizando fórmulas diferentes a las anteriores.
La población no refiere únicamente a individuos. Si la población está claramente definida como las top 10 empresas de Forbes, y el análisis descriptivo específica que se usarán esas diez para el estudio, resulta apropiado aplicar las fórmulas poblacionales para la varianza y el desvío estándar.
Donde X raya es la media muestral, y n-1 refiere a los grados de libertad cuando se estima la varianza poblacional.
Desviación estándar muestral
Donde X raya es la media muestral.
Semi-Varianza y Semi-Desviación
La varianza o desviación estándar de los retornos son usualmente interpretados como medidas de riesgo de un activo. Contemplan las dispersiones por arriba, y por abajo, de la media, pero los inversores están únicamente preocupados con el riesgo debajo (retornos por abajo de la media). Como resultado, se ha desarrollado la semi-varianza y semi-desviación.
Para el cómputo:
1) Calcular la media muestral
2) Identificar las observaciones que son menores a la media (descartar las observaciones que son igual o mayores a la media); suponer n* observaciones menores a la media.
3) Computar la sumatoria del cuadrado de las dispersiones en torno a la media.4) Dividir por n*-1. La fórmula para la semi-varianza es:
La desviación estándar es más sencilla de interpretar que la varianza, ya que está expresada en las mismas unidades que las observaciones (en la varianza, las observaciones se elevan al cuadrado). Podemos encontrarnos con que es difícil interpretar que significa la desviación estándar en términos de variabilidad cuando miramos diferentes set de datos, debido a que cada set de datos posee una media diferente, o los otros set de datos pueden estar expresados en diferentes unidades. El coeficiente de variación resulta una herramienta útil en estas situaciones. Por ello, es que se referencia al coeficiente de variación como una medida de dispersión relativa.
A continuación, ilustramos un ejemplo de dos set de muestras, con medias marcadamente diferentes.
Muestra A: 50, 75, 65, 90
Media muestral: 70
Desvío muestral: 16,8
Muestra B: 800, 825, 815, 840
Media muestral: 820
Desvío muestral: 16,8
En la primera muestra, la observación más grande, 90, es un 80% más grande que la observación más chica, 50.
En la segunda muestra, la observación más grande, 840, es un 5% más grande que la observación más chica, 800.
Informalmente, un desvío muestral de 16,8 refleja un alto nivel de variabilidad relativa a la primera muestra, cuya media es 70. Pero un bajo nivel de variabilidad relativa a la segunda, cuya media es 820.
El coeficiente de variación puede calcularse a través de:
Donde S denota la desviación muestral, y X raya la media muestral.
Si calculamos el coeficiente de variación para ambas muestra, obtenemos que:
CV(A) = 0,24
CV(B) = 0,02
Lo que confirma nuestra intuición de que la muestra A exhibe una mayor variabilidad que la segunda muestra. Además, al dividir el desvío sobre la media, que es medida en las mismas unidades que la desviación estándar, el coeficiente de variación está libre de unidades de medición, y permite comparar la variabilidad de variables expresadas en distintas unidades.
Ratio de Sharpe
Si tomamos la inversa del coeficiente de variación, y sea por ejemplo, la media de los retornos 1.19% y la desviación estándar 4.42%, tenemos 1,19%/4,42% = 0,27. Este resultado indica que cada unidad de desvío estándar representa un 0,27% de retorno -- el retorno por unidad de riesgo.
Una medida más precisa de riesgo-retorno contempla la existencia del "retorno libre de riesgo" (risk free return -- los bonos del tesoro de EE.UU), es decir un retorno que posee cero desviación estándar. La fórmula del Ratio de Sharpe es:
Donde R raya-sub-p denota el retorno medio del portafolio y R raya-sub-f el retorno medio del activo libre de riesgo. La intuición es que el numerador refleja los valores medios, tal como la inversa del coeficiente de variación. S sub-p refleja el desvío estándar del portafolio.
El numerador denota el exceso de retorno, de invertir en un activo riesgoso. Es la recompensa de invertir en el riesgo. El denominador refleja el riesgo. Por ende, el ratio de Sharpe refleja el exceso de retorno, por unidad de riesgo.
A mayor ratio de Sharpe, más premiados estarán los inversores, por unidad de riesgo. Es importante mencionar que es posible que el resultado del ratio sea negativo, esto se dará generalmente en períodos donde el mercado de acciones esté en tendencia bajista (bearish), y aquí debe tenerse sumo cuidado al interpretar el resultado: si con un ratio de Sharpe positivo, incrementamos el riesgo, el ratio resultará más alto. Sin embargo, con un ratio de Sharpe negativo, si aumentamos el riesgo (lo duplicamos), el resultado pasará de -1 a -0,5. Por eso cuando comparemos portafolios con ratio de Sharpe negativos, no podemos interpretar que el mayor ratio es mejor. En este caso, quizás debamos incrementar el período contemplado, hasta lograr un ratio de Sharpe positivo.







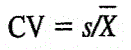



Comentarios
Publicar un comentario